

资讯动态
neotrident news
资讯动态
本文旨在教给大家通过phoenix winnonlin中实现tmdd模型的建立,包含partial mm消除的经验模型和full tmdd/qe/qss等模型,并且对几种模型的选择提供一些参考。
1993 年,gerhard levy 首先提出了靶点介导的药物处置( target mediated drug disposition,tmdd) 理论,用于描述药物与生物靶点(例如,受体)的高亲和力的现象,并阐述tmdd对药物体内药代动力学(pk)和药效动力学(pd)的影响。 一般小分子药物在体内靶点饱和的情况在模型拟合中经常被忽略,是因为在血浆或者组织中非特异性靶点容量很大,很难被饱和。某些药物,特别是单抗大分子药物,由于其分子量大,药物分布和消除都和一般药物具有很大不同,且具有靶点特异性,那么靶点介导的药物处置过程就不容忽视。
下图为大分子单抗不同剂量下的典型药时曲线(浓度取对数),通常我们将其分成4个阶段,第一阶段:药物与靶点间快速形成平衡;第二阶段:靶点处于饱和状态,药物主要通过异化作用消除,一级动力学,所以曲线呈现线性特征;第三阶段:靶点的饱和状态逐步减弱,此时靶点介导药物处置,这一消除途径的影响越来越明显,总体呈现为非线性 pk;第四阶段:药物浓度进一步降低,靶点远未达饱和,靶点介导的消除和异化作用都为一级动力学过程,总体又呈现为线性pk [1]。
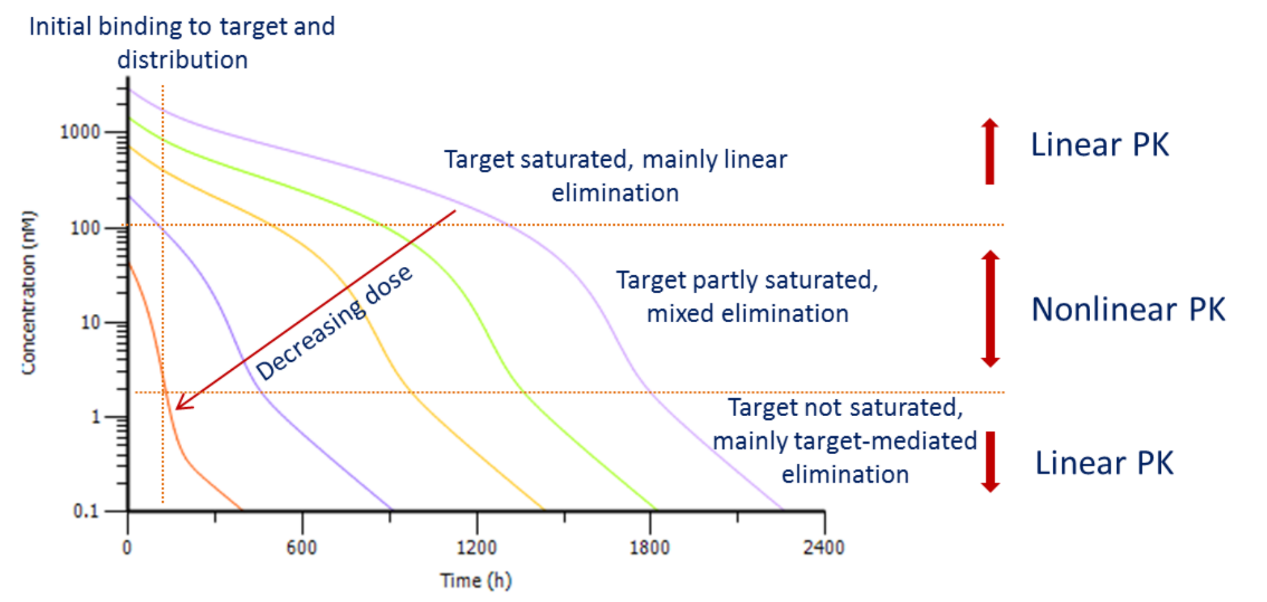
图 | 大分子单抗不同剂量下的典型药时曲线(浓度取对数)
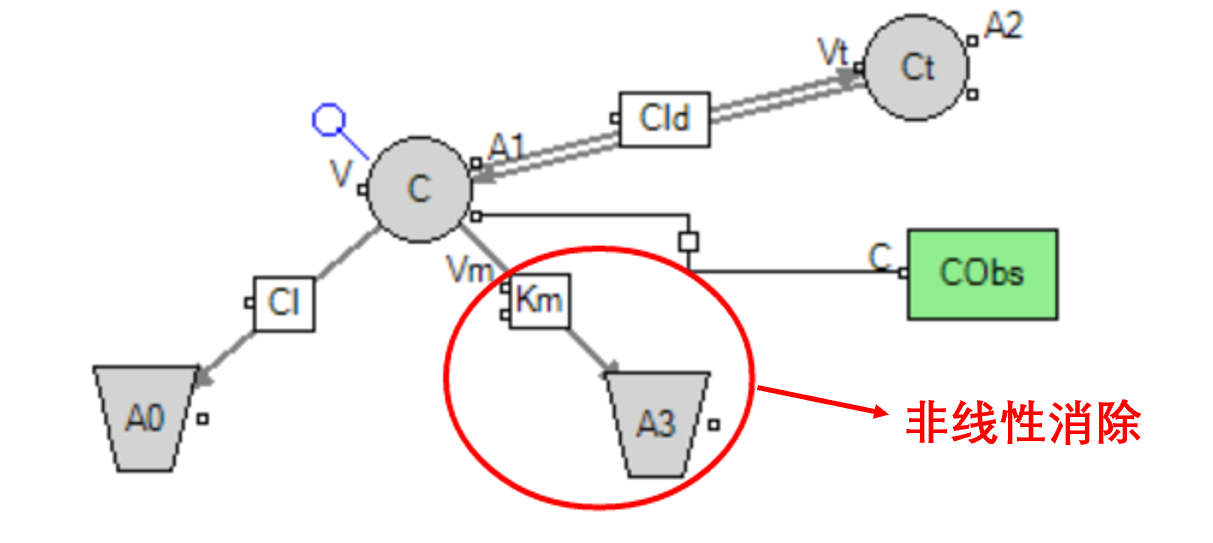
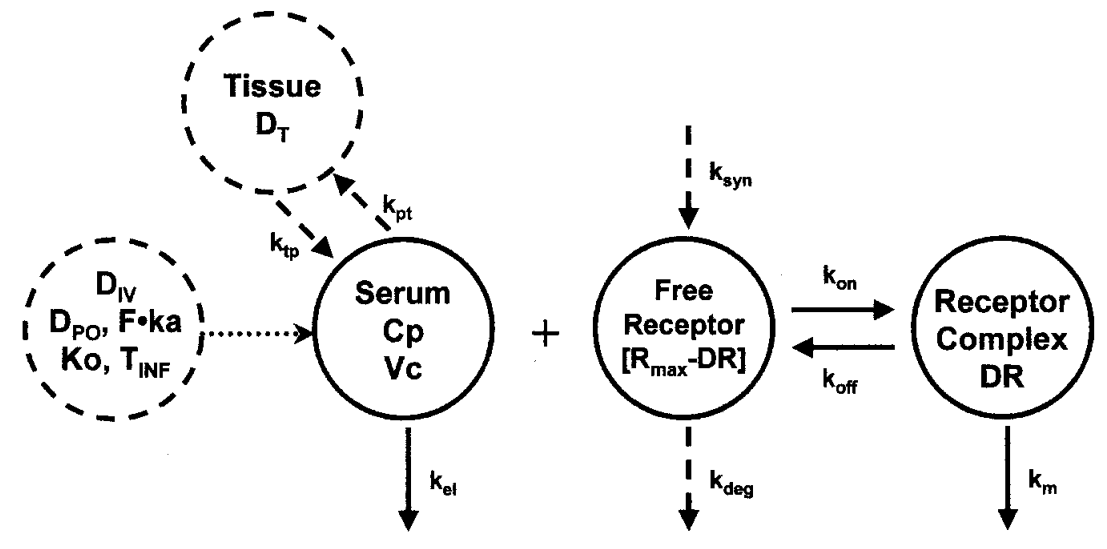
全tmdd模型对应的微分方程:

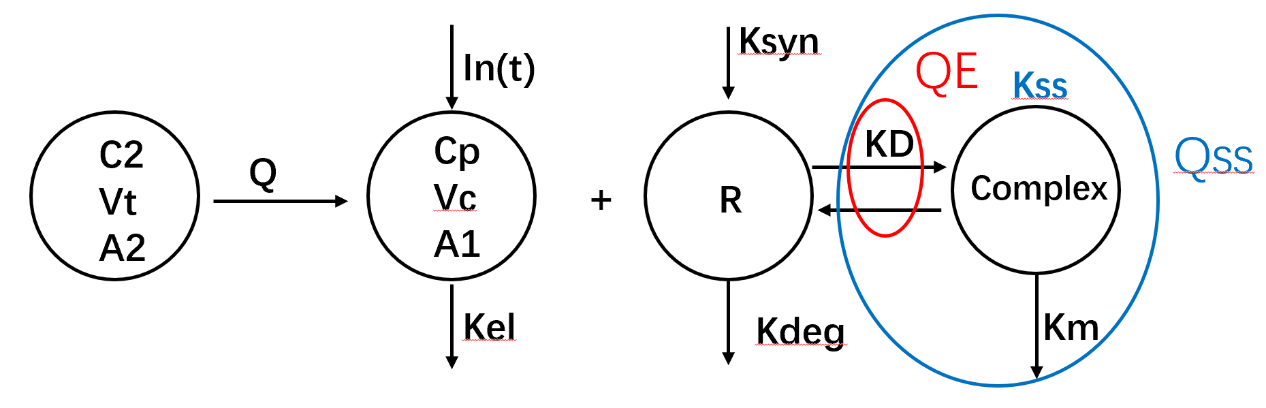
qe近似模型:配体-受体结合和解离比其余的系统过程快几个数量级,所以可以假设km(复合物内化)远小于koff(解离) ,通过一个解离平衡常数kd来代替kon和koff,完成模型简化:
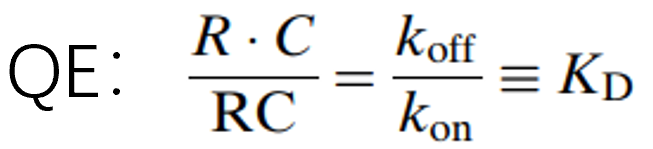
qss近似模型:接着还可以把复合物内化速率和配体-受体结合解离看成一个整体,用kss表示(复合物内化消除速率和结合-解离速率相当,不可忽略),就简化为qss模型:
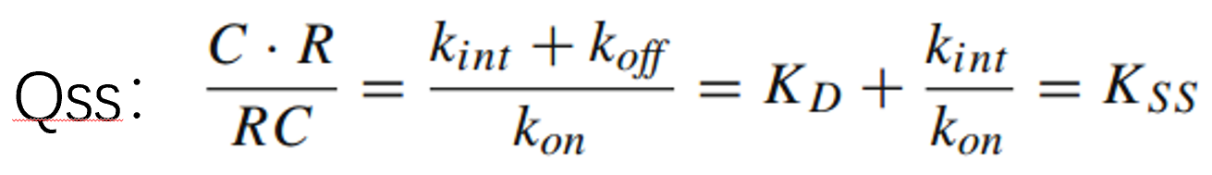
本教程使用的数据和代码可以通过关注创腾科技公众号,回复关键词:tmdd获取
a) 准备数据:
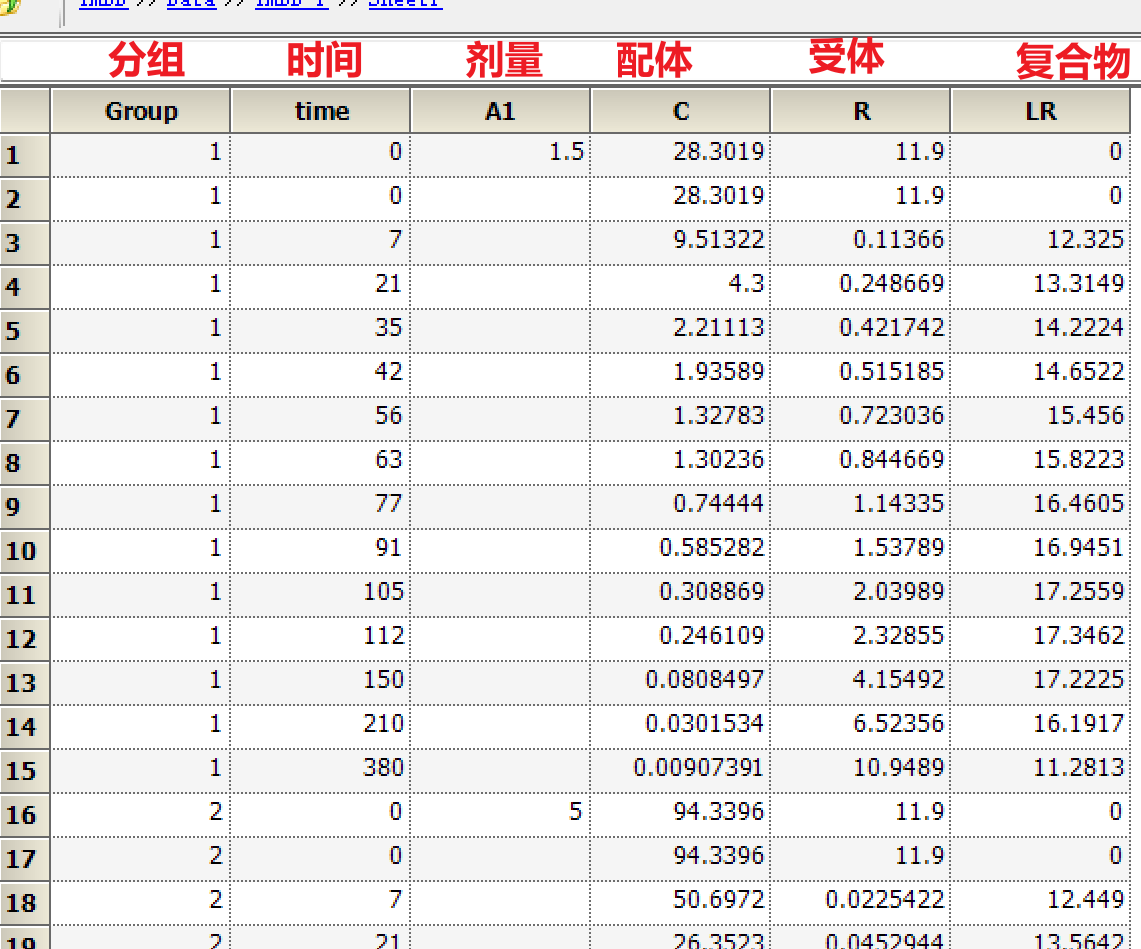
b) 注意图中标红的部分,这是tmdd(或者非线性消除)的典型特征,最好能够有不同剂量的pk数据,因为剂量太低或者太高,tmdd特征都不是很明显。打开phoenix winnonlin软件,file→new project,import 准备好的数据,将数据发送到xy plot作图:
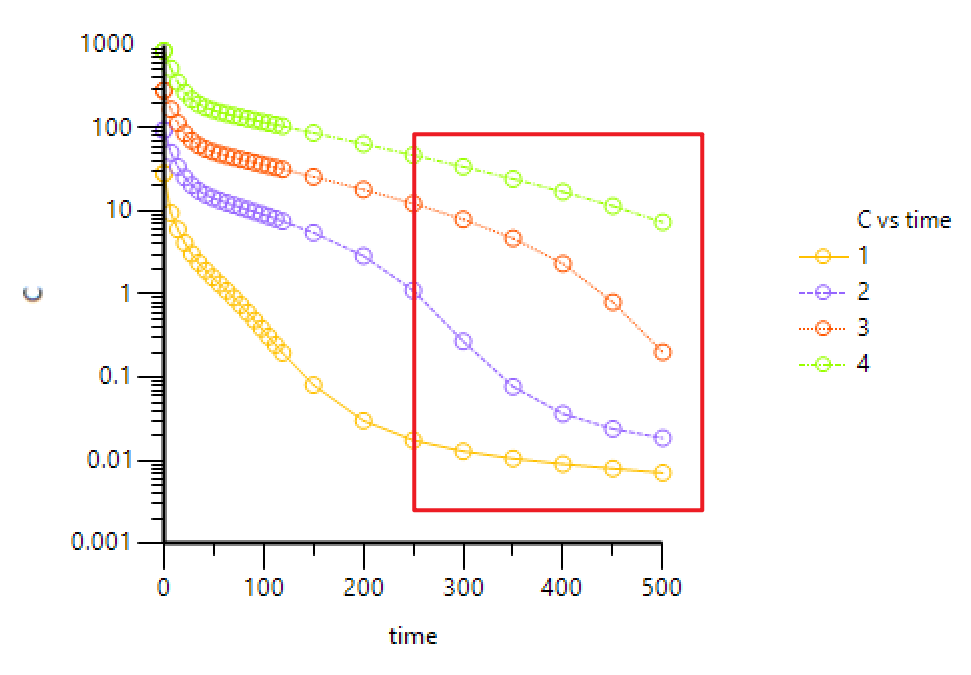
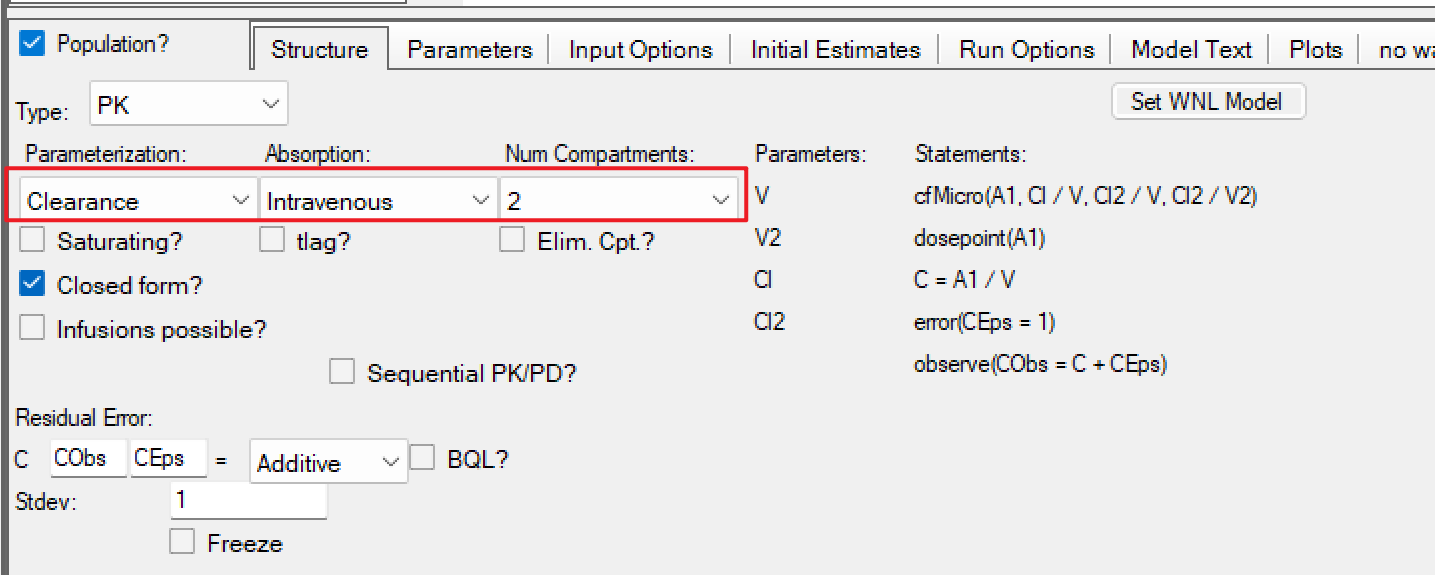
c) 将数据send to→phoenix model(maximum likehood model),先设置静脉二房室的基础模型
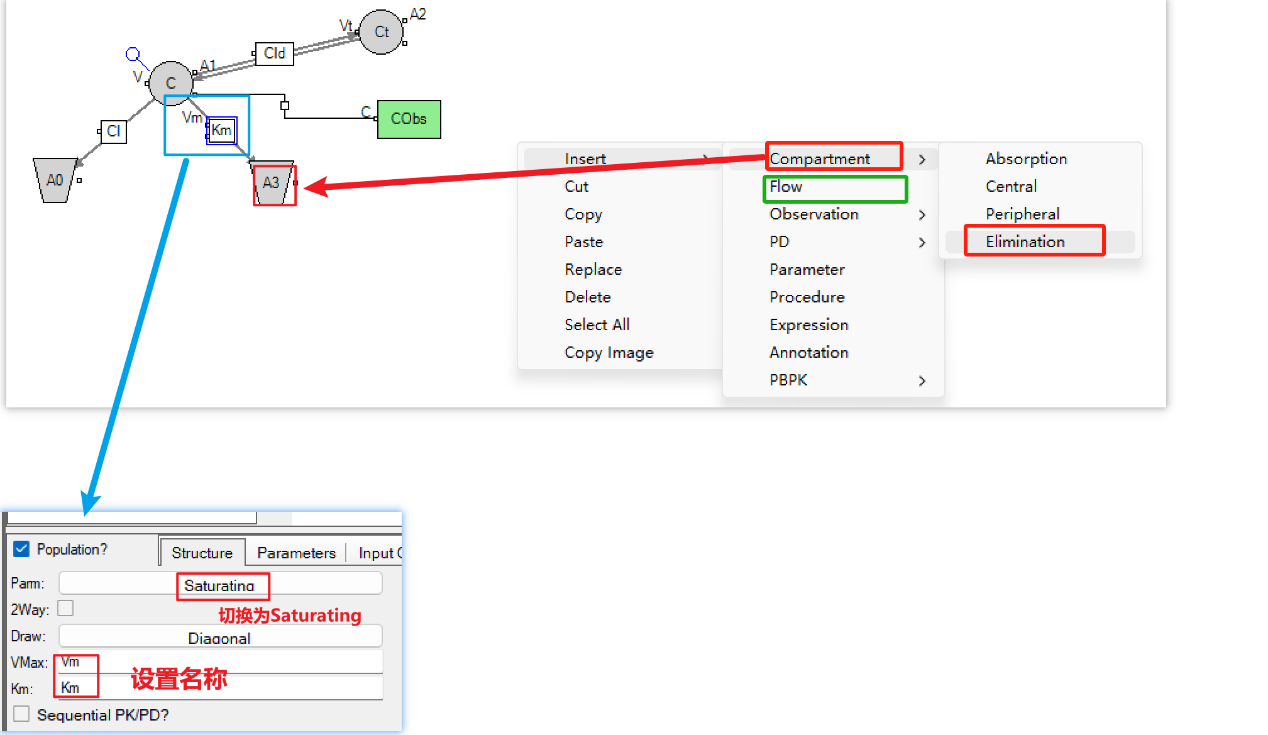
d) 随后点击右侧的edit as graphical转成图形编辑模式,添加一条新的消除途径, 并将其设置为saturating。
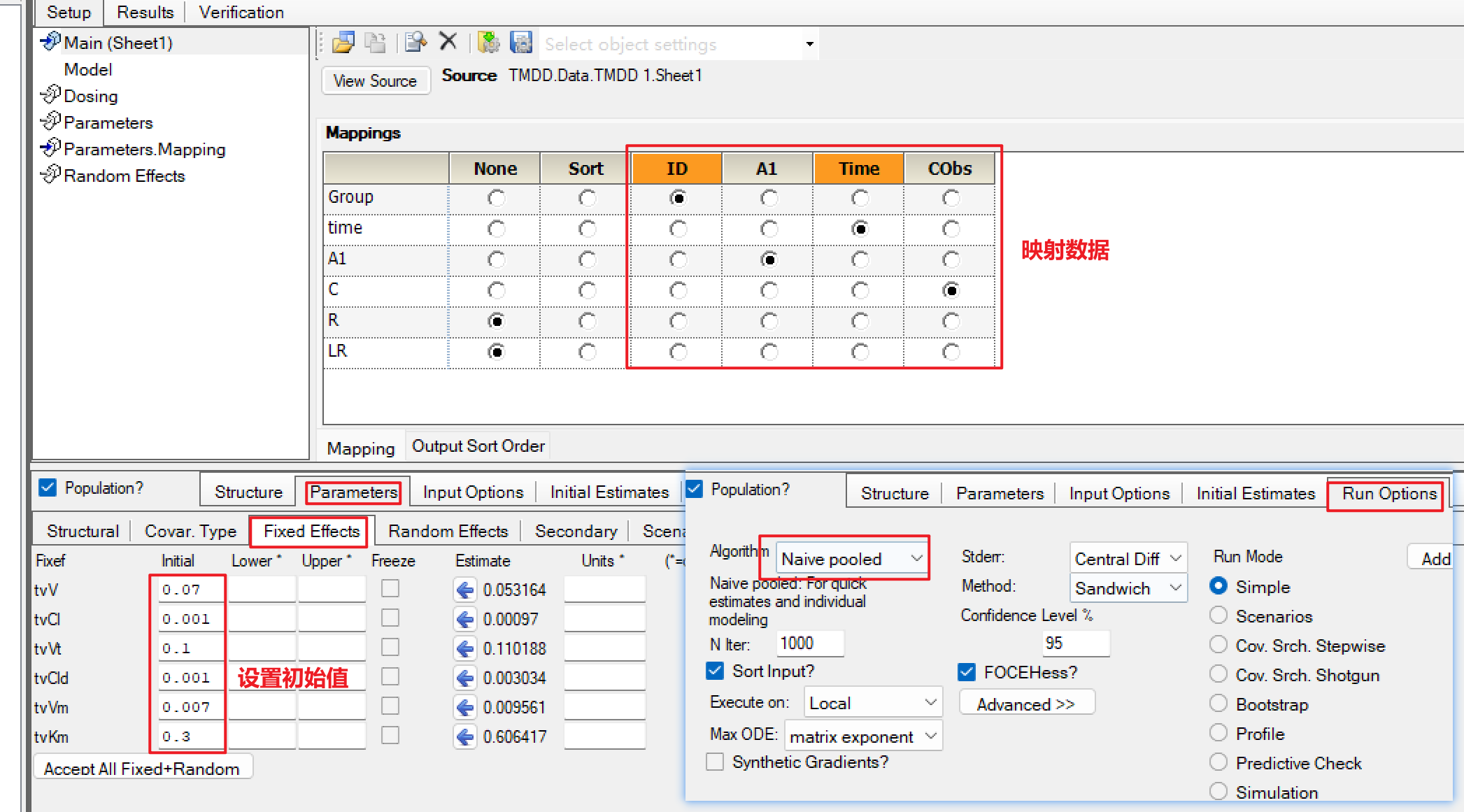
e)映射好数据,设置好初始值,将算法设置为naïve pool。
f) 运行该任务,即可查看拟合结果。
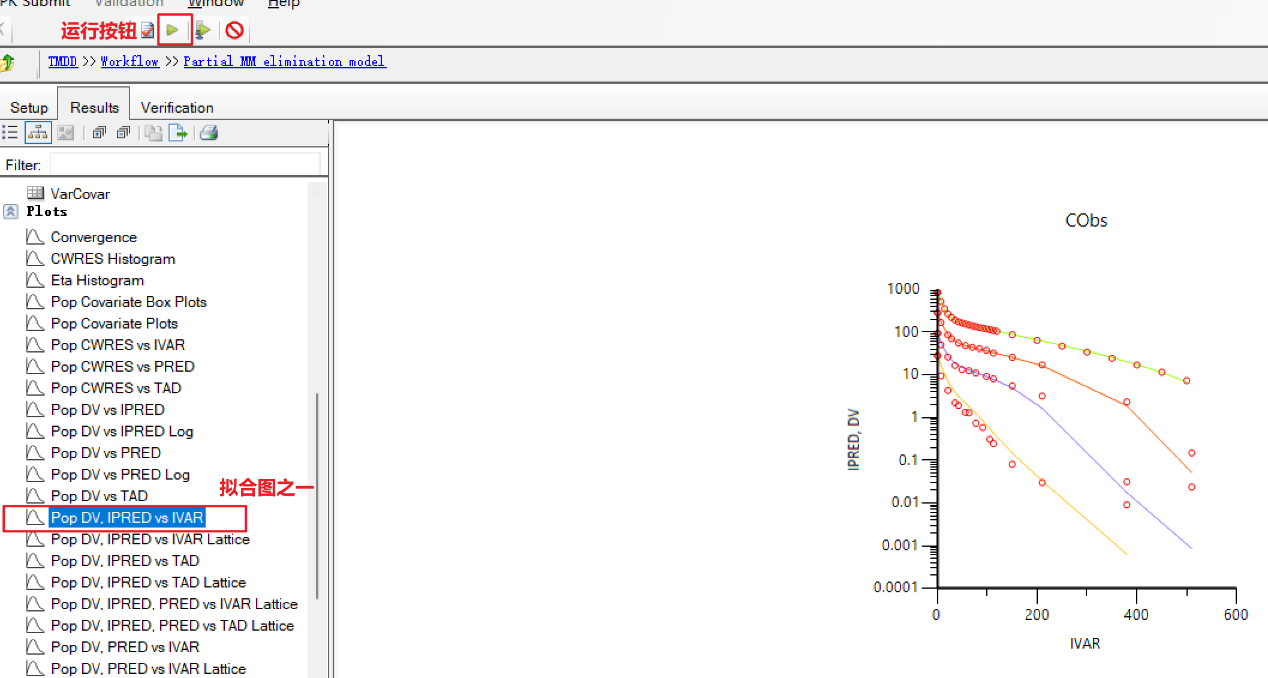
a) 还是上面的数据,send to→phoenix model(maximum likehood model),点击右边的edit as textual切换成代码模式:
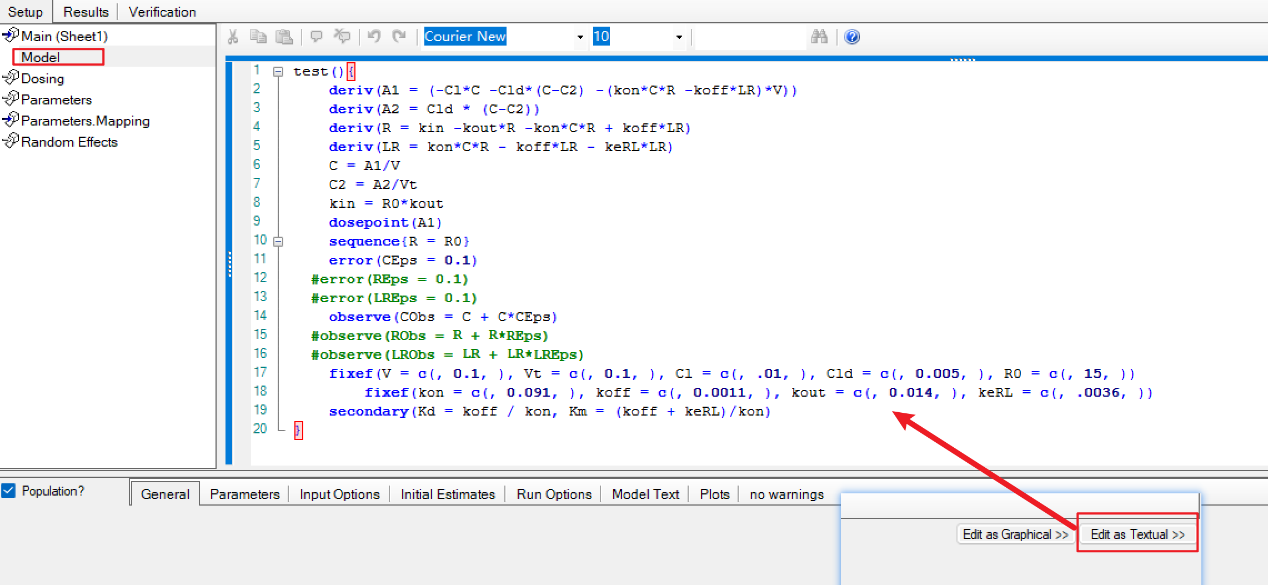
b) 在model中替换为以下代码[3]:
test(){
deriv(a1 = (-cl*c -cld*(c-c2) -(kon*c*r -koff*lr)*v))
deriv(a2 = cld * (c-c2))
deriv(r = kin -kout*r -kon*c*r koff*lr)
deriv(lr = kon*c*r - koff*lr - kerl*lr)
c = a1/v
c2 = a2/vt
kin = r0*kout
dosepoint(a1)
sequence{r = r0}
error(ceps = 0.1)
#error(reps = 0.1) #当需要增加该观测变量时,去掉前面的井号;
#error(lreps = 0.1) #当需要增加该观测变量时,去掉前面的井号;
observe(cobs = c c*ceps)
#observe(robs = r r*reps)#当需要增加该观测变量时,去掉前面的井号;
#observe(lrobs = lr lr*lreps) #当需要增加该观测变量时,去掉前面的井号;
fixef(v = c(, 0.1, ), vt = c(, 0.1, ), cl = c(, .01, ), cld = c(, 0.005, ), r0 = c(, 15, ))
fixef(kon = c(, 0.091, ), koff = c(, 0.0011, ), kout = c(, 0.014, ), kerl = c(, .0036, ))
secondary(kd = koff / kon, km = (koff kerl)/kon)
}
备注:
· 前面带#号的 "observe()" 和 "error()" 是成对的,增加对应的观测变量时,成对的"observe()" 和 "error()" 前面的#号要求一起去掉;
· fixef()语句是表示参数初值设置的地方
c) 在main中进行数据映射,run options中将算法设置为naïve pool
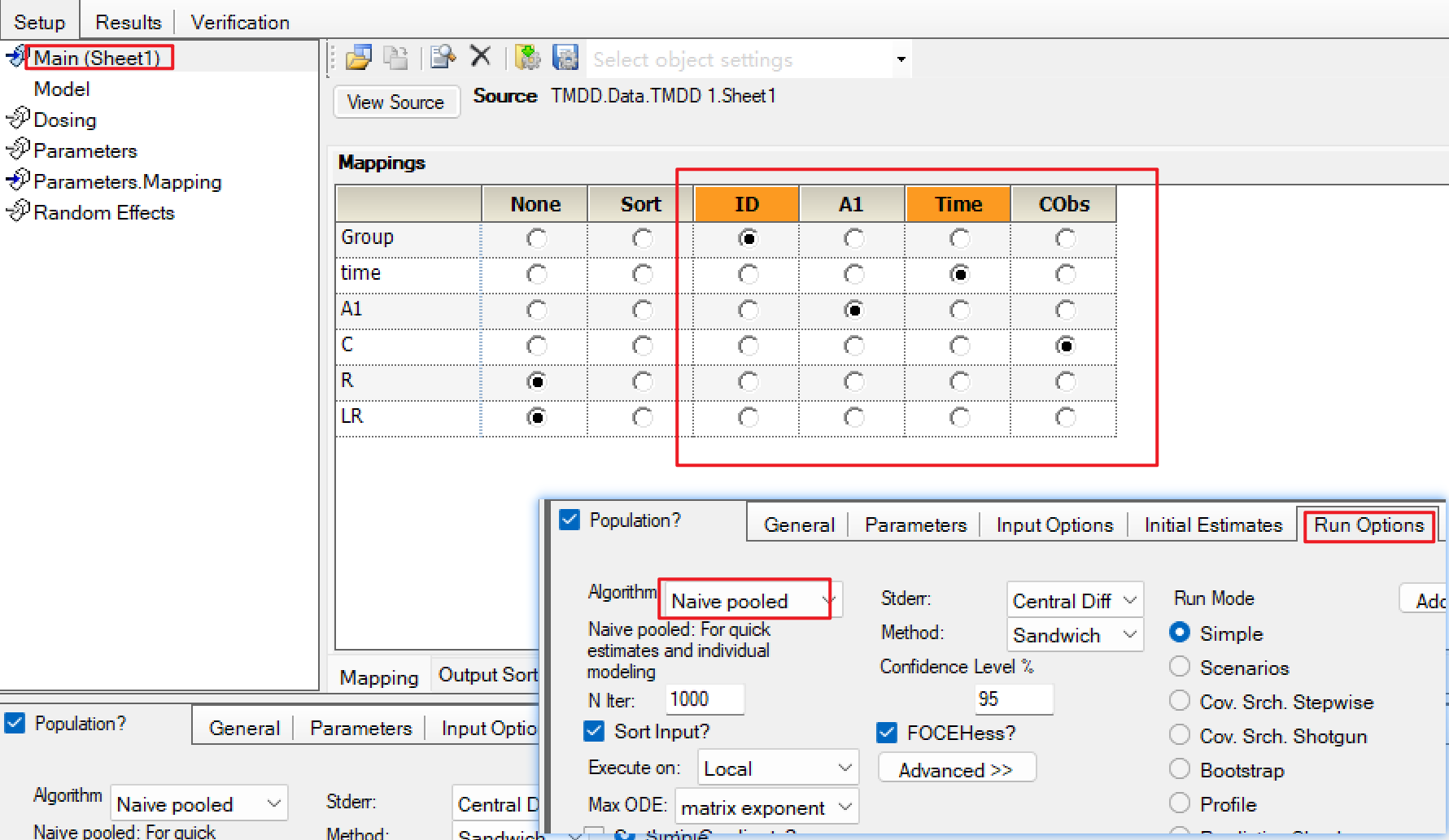
d) 运行该任务,查看结果:我们可以对比一下分别提供c,c r和c r lr观测值的拟合结果:
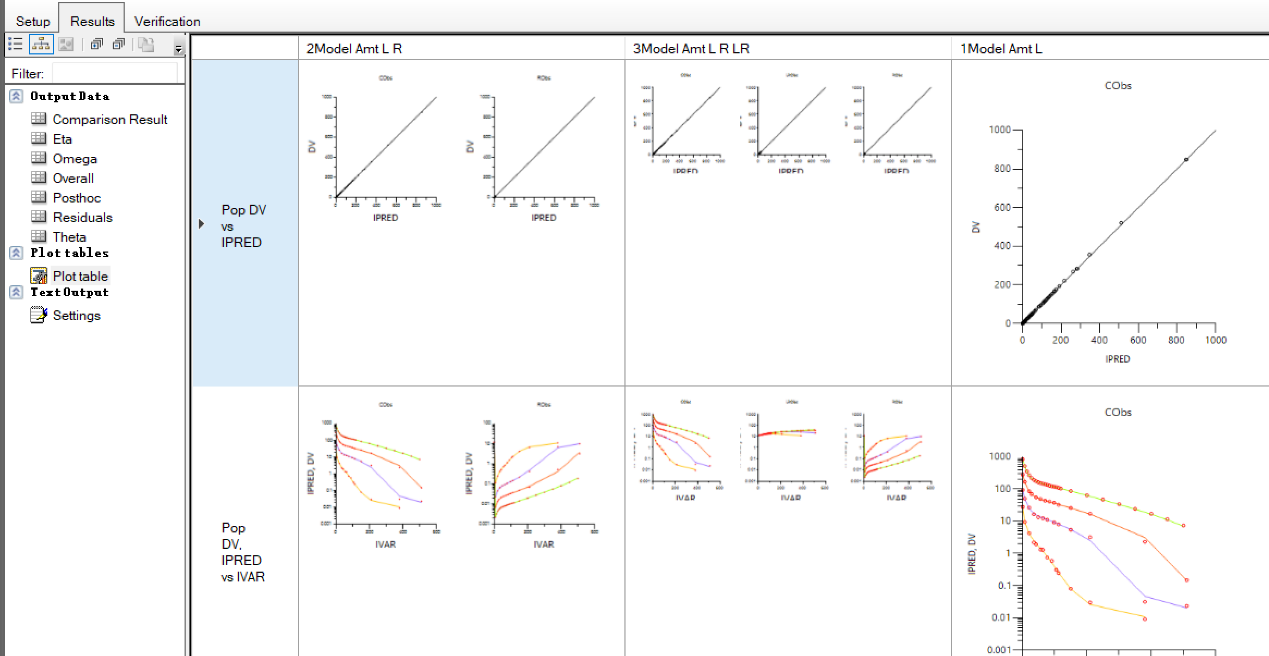

我们从拟合图看到,你和效果差不多,但是从参数 (theta)结果可以看到,当用户提供的信息越多,越丰富,参数拟合的精度也越高(rse%越小)。但是通常来说,大多数时候,我们只有配体的数据,这也是在做full tmdd模型时候的困境。
当数据有限时,比如只有配体的数据,那么qe/qss等简化tmdd模型[4][5],或许是不错的选择。tmdd简化模型原理我们在第二部分常用模型中已经介绍,使用方法依然是复制代码至model中使用,和前面的full tmdd模型相同,代码如下:
1. qe模型pml代码:
test(){
#adapted from gibiansky et al. 2008 journal of pharmacokinetics and pharmacodynamics". parameterized for cl.
dosepoint(atot)
#给药剂量单位应换算为 pmol/kg. pmol (dose) / ml (volume) = nm. 对于分子量为150kda的分子来说,6700 pmol/kg 约等于 1 mg/kg
deriv(atot = (-kint*ctot -((cl/v1) (q/v1)-kint)*c1)*v1 q*c2)
kint = kdeg
ctot = atot / v1
c1 = 1/2*((ctot-rtot-kd) sqrt((ctot-rtot-kd)^2 4*kd*ctot))
cugml = c1*0.15
#假设分子量为150kda,将nm转换为观测数据的ug/ml的单位,如果分子不是150kda,请按照实际分子量设置此处。
deriv(a2 = q*c1 - q*c2)
c2 = a2/v2
#target:靶点部分的代码
ksyn = r0 * kdeg
deriv(rtot = ksyn - kdeg*rtot-(kint-kdeg)*(ctot-c1) )
complex = rtot*c1/(kd c1)
rfree = rtot - complex
ropercent = complex / rtot * 100
error(ceps=0.1)
observe(cobs = cugml*(1 ceps))
sequence{
rtot = r0
}
stparm(v1 = tvv1)
stparm(v2 = tvv2)
stparm(r0 = tvr0)
stparm(cl = tvcl)
stparm(q = tvq)
stparm(kd = tvkd)
#stparm(kint = tvkint)
#degradation/internalization of complex. add this to the model if the degradation of complex is different from degradation of free receptor
stparm(kdeg = tvkdeg)
# degradation of receptor.
fixef(tvr0 = c(, 12,)) # nm; steady state conc of the receptor
fixef(tvv1 = c(, 0.05, )) # ml/kg; volume of central comp
fixef(tvv2 = c(, 0.1, )) # ml/kg; volume of peripheral comp
fixef(tvcl = c(, 0.001, )) # ml/kg/d; clearance
fixef(tvq = c(, 0.003, )) # ml/kg/d; intercompartmental clearance
fixef(tvkd = c(, 9, )) # nm; kd = dissociation constant = koff/kon
#fixef(tvkint = c(,0.2,)) #degradation of complex. add this to the model if the degradation of complex is different from degradation of free receptor
fixef(tvkdeg = c(, 0.003, )) # 1/d; degradation rate of receptor. t1/2 = ln2/kdeg.
}
2. qss模型pml代码:
test(){
#adapted from gibiansky et al. 2008 journal of pharmacokinetics and pharmacodynamics". parameterized for cl.
dosepoint(atot) #给药剂量单位应换算为 pmol/kg. pmol (dose) / ml (volume) = nm. 对于分子量为150kda的分子来说,6700 pmol/kg 约等于 1 mg/kg
#mab
deriv(atot = (-kint*ctot -((cl/v1) (q/v1)-kint)*c1)*v1 q*c2) #总药量变化微分方程
kint = kdeg
ctot = atot / v1
c1 = 1/2*((ctot-rtot-kss) sqrt((ctot-rtot-kss)^2 4*kss*ctot))
cugml = c1*0.15
deriv(a2 = q*(c1 -c2))
c2 = a2/v2
#target:靶点部分的代码
ksyn = r0 * kdeg
deriv(rtot = ksyn - kdeg*rtot-(kint-kdeg)*complex )
complex = rtot*c1/(kss c1)
rfree = rtot - complex
ropercent = complex / rtot * 100
error(ceps=0.1)
observe(cobs = cugml*(1 ceps))
sequence{
rtot = r0
}
stparm(v1 = tvv1)
stparm(v2 = tvv2)
stparm(r0 = tvr0)
stparm(cl = tvcl)
stparm(q = tvq)
stparm(kss = tvkss)
#stparm(kint = tvkint) #degradation/internalization of complex. add this to the model if the degradation of complex is different from degradation of free receptor
stparm(kdeg = tvkdeg) # degradation of receptor.
fixef(tvr0 = c(, 12,)) # nm; steady state conc of the receptor
fixef(tvv1 = c(, 0.05, ))# ml/kg; volume of central comp
fixef(tvv2 = c(, 0.1, ))# ml/kg; volume of peripheral comp
fixef(tvcl = c(, 0.001, ))# ml/kg/d; clearance
fixef(tvq = c(, 0.003, )) # ml/kg/d; intercompartmental clearance
fixef(tvkss = c(, 9, ))# nm; kss = steady state constant =(koff kint)/kon
#fixef(tvkint = c(,0.2,)) #degradation of complex. add this to the model if the degradation of complex is different from degradation of free receptor
fixef(tvkdeg = c(, 0.003, )) # 1/d; degradation rate of receptor. t1/2 = ln2/kdeg.
}
治疗性单克隆抗体的典型参数范围

上表是一些单克隆抗体参数的参考范围,可以通过这个表格来换算一些参数的初值。另外,一些配体受体亲和力参数,比如kon,koff,kdeg等可以参考非临床或者体外试验的一些结果,可以更好的帮助大家获取参数初值。
上面提到的多个模型,结合文献[6],我们可以对模型的选择做个总结:
1. 从研究目的出发:
· 如果目的是为了首次临床剂量的推算,那么完整的tmdd或者基于生理的tmdd模型更加合适。
· 如果研究目的是为了预测数据进行末端半衰期的计算,qss模型将不是合理的选择,因为它不能准确预测药物末端相的药动学行为,此时qe将是更好的选择。
2. 考虑获取数据的局限:
· 只有配体浓度数据时,简化的tmdd模型或经验模型是更好的选择
· 如果游离受体浓度远大于药物浓度时,则qe模型可能是无效的,准确性无法保证(主要是低剂量的时候)
· 数据信息量比较不足时,采样点不充分,时间不够长,mm经验模型或许是一种稳健的选择。
总之,我们可以根据目的和数据情况,综合判断可以选择哪些模型来做。
本教程使用的数据和代码可以通过关注创腾科技公众号,回复关键词:tmdd获取

参考文献:
1. peletier l a, gabrielsson j. dynamics of target-mediated drug disposition: characteristic profiles and parameter identification[j]. journal of pharmacokinetics and pharmacodynamics, 2012, 39: 429-451.
2. gabrielsson j, weiner d. pharmacokinetic and pharmacodynamic data analysis, concepts and applications, 5th ed.
3. mager d e, jusko w j. general pharmacokinetic model for drugs exhibiting target-mediated drug disposition[j]. journal of pharmacokinetics and pharmacodynamics, 2001, 28: 507-532.
4. mager d e, krzyzanski w. quasi-equilibrium pharmacokinetic model for drugs exhibiting target-mediated drug disposition[j]. pharmaceutical research, 2005, 22: 1589-1596.
5. gibiansky l, gibiansky e, kakkar t, et al. approximations of the target-mediated drug disposition model and identifiability of model parameters[j]. journal of pharmacokinetics and pharmacodynamics, 2008, 35: 573-591.